Posts Tagged with "ISO 26262"
既に発行済みのブログであっても適宜修正・追加することがあります。
We may make changes and additions to blogs already published.
posted by sakurai on November 5, 2019 #176
- シナリオ3:FTTI内の危険事象を防ぐ安全機構が実装されたシステム。ただし、安全な状態に移行するには緊急操作が必要です。車両の動作状態を制限することにより、緊急動作許容時間内に安全状態が達成されます。
$$ T_\text{FDTI}+T_\text{FRTI}<T_\text{FTTI}かつ\\
T_\text{EOTI}<T_\text{EOTTI}$$
モーターがショートすると、バルブが最大位置に達します。実装された安全機構によりバルブモーターの電源がオフになり、メカニカルスプリングがバルブをFTTI内の低流量位置に戻します。安全機構(スプリング)は、限られた時間だけ動作するように設計されています(EOTTI)。 EOTTIの有効期限が切れる前に、車両の動作状態が制限されているため、バルブからの流れが危険事象を引き起こすことはありません。
- シナリオ4:FTTI内に危険事象を防ぐ安全機構が実装されたシステムですが、安全状態に移行するには緊急操作が必要です。ただし、移行時間はEOTTIより長くかかります。結果として、累積リスクは受け入れられなくなり、機能安全コンセプトで指定された目標を超えます。
$$ T_\text{FDTI}+T_\text{FRTI}<T_\text{FTTI}かつ\\
T_\text{EOTTI}<T_\text{EOTI}$$
モーターがショートすると、バルブが最大位置に達します。実装された安全機構によりバルブモーターの電源がオフになり、メカニカルスプリングがバルブをFTTI内の低流量位置に戻します。安全機構(スプリング)は、限られた時間だけ動作するように設計されています(EOTTI)。このシナリオでは、車両の動作は制限されておらず、アイテムはEOTTIの有効期限よりも長く緊急動作しているため、安全目標違反の不当なリスクが生じます。
以上より、EOTTIは、安全機構がFTTIを超えて安全を担保しているとき(VSGを抑止しているとき)、安全機構の構造により担保時間(抑止時間)に制約がある場合、その制約の期間を意味します。従って、その制約時間内に修理するか、あるいは別の、例えばスタンバイ機構により機能が継続できなければ、安全機構の効果が無くなり、VSGとなってしまいます。仮に修理工場に持っていく場合は、EOTTIとして数百時間が必要となります。
 前のブログ
次のブログ
前のブログ
次のブログ
posted by sakurai on October 31, 2019 #175
2nd EditionのPart 10の4.4.2のタイミングモデルを解説します。ここでは例としてモータ制御システムを取り上げています。ただし、数式は本ブログ独自の記述です。
以下に各種時間制約を列挙します。
- $T_\text{FDTI}$:障害検出時間間隔(FDTI)
- $T_\text{FTTI}$:耐障害時間間隔(FTTI)
- $T_\text{FRTI}$:障害反応時間間隔(FRTI)
- $T_\text{EOTTI}$:緊急操作許容時間間隔(EOTTI)
- $T_\text{DTTI}$:診断テスト時間間隔(DTTI)
バルブ制御システムの例。
このシステムは、バルブ、位置センサー、コントローラー、電気モーターで構成されています。システムの機能は、電気モーターを使用してバルブを所望の位置に制御することです。
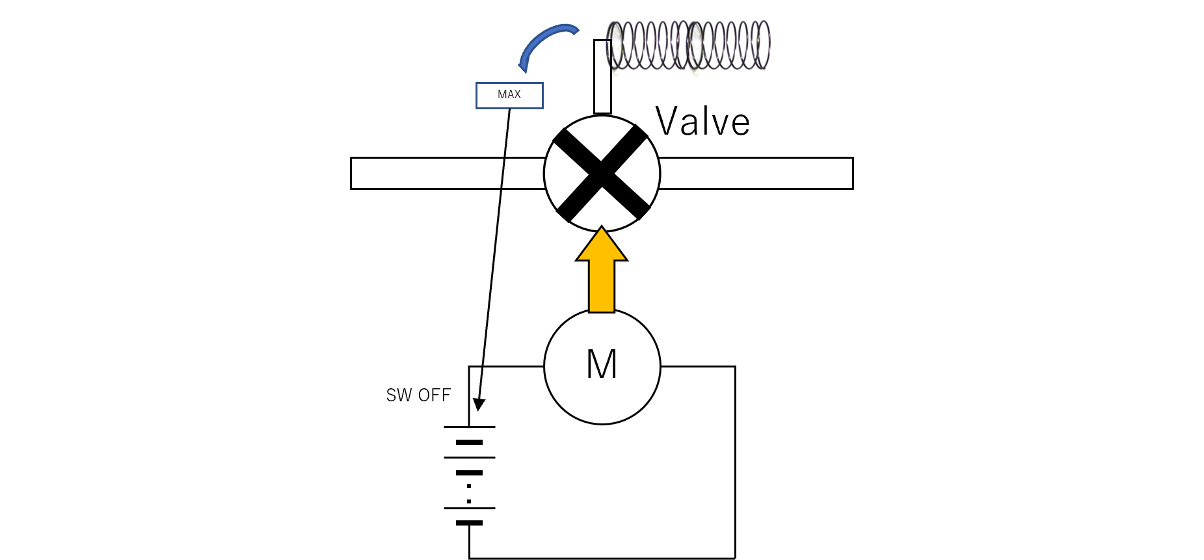 図175.1 システム例
図175.1 システム例
バルブが意図した以上に開いた場合、意図しない流れに起因する危険なイベントが発生する可能性があります。故障反応として、モーターは、バルブをデフォルトの固定開位置に引っ張る機械的スプリングと組み合わせた別個の回路によって電源が切断されます。この固定されたバルブ位置は流れを制限するため、その結果、アイテムは安全状態になります。
シナリオ1:安全機構が一切無い場合です。モーターがショートすると、バルブは最大位置に達します。安全機構がないため、FTTIを超える危険なイベントが発生する可能性があります。
$$ T_\text{FTTI}<T_\text{FDTI}+T_\text{FRTI}=\infty$$
シナリオ2:緊急操作を行わずに安全機構を実装したシステムにより、安全状態がFTTI内で達成されます。
$$ T_\text{FDTI}+T_\text{FRTI}<T_\text{FTTI}かつ\\
T_\text{EOTI}<T_\text{EOTTI}=\infty$$
モーターがショートすると、バルブは最大位置に達します。すると、実装された安全機構によりバルブモーターの電源がオフになり、FTTI内でメカニカルスプリングがバルブを低流量位置に戻し、危険なイベントを防ぎます。安全機構(スプリング)は無期限に動作するように設計されており、従って安全状態は無限に続きます。
 前のブログ
次のブログ
前のブログ
次のブログ
posted by sakurai on October 28, 2019 #174
- 箱(v)ではMPFの検出率を聞いています。これも条件付き確率$\Pr\{\text{fault detected}\ |\ \text{fault occured}\}$ではありません。故障率や故障数に依らない、アーキテクチャで決まった定数です。
検出された部分(detected)は下左に移動し、箱(w)で検出率$K_{FMCi,MPF}$を掛けられ$\lambda_{FMCi,MPF,det}$と名付けられます。次に下に移動し、箱(x)でMPF detected故障率として分類されます。$\dagger$
$$
\lambda_{FMi,MPF,det}=K_{FMCi,MPF}\lambda_{FMi,MPF}\tag{w, x}
$$
一方、検出されない部分(not detected)は下に移動し、箱(y)で不検出率$1-K_{FMCi,MPF}$を掛けられ、$\lambda_{FMCi,MPF,pl}$と名付けられます。
$$
\lambda_{FMi,MPF,pl}=(1-K_{FMCi,MPF})\lambda_{FMi,MPF}\tag{y}
$$
次の箱(z)では、ドライバーに認識される率を聞いています。認識率を$F_{FMC,per}$とします。
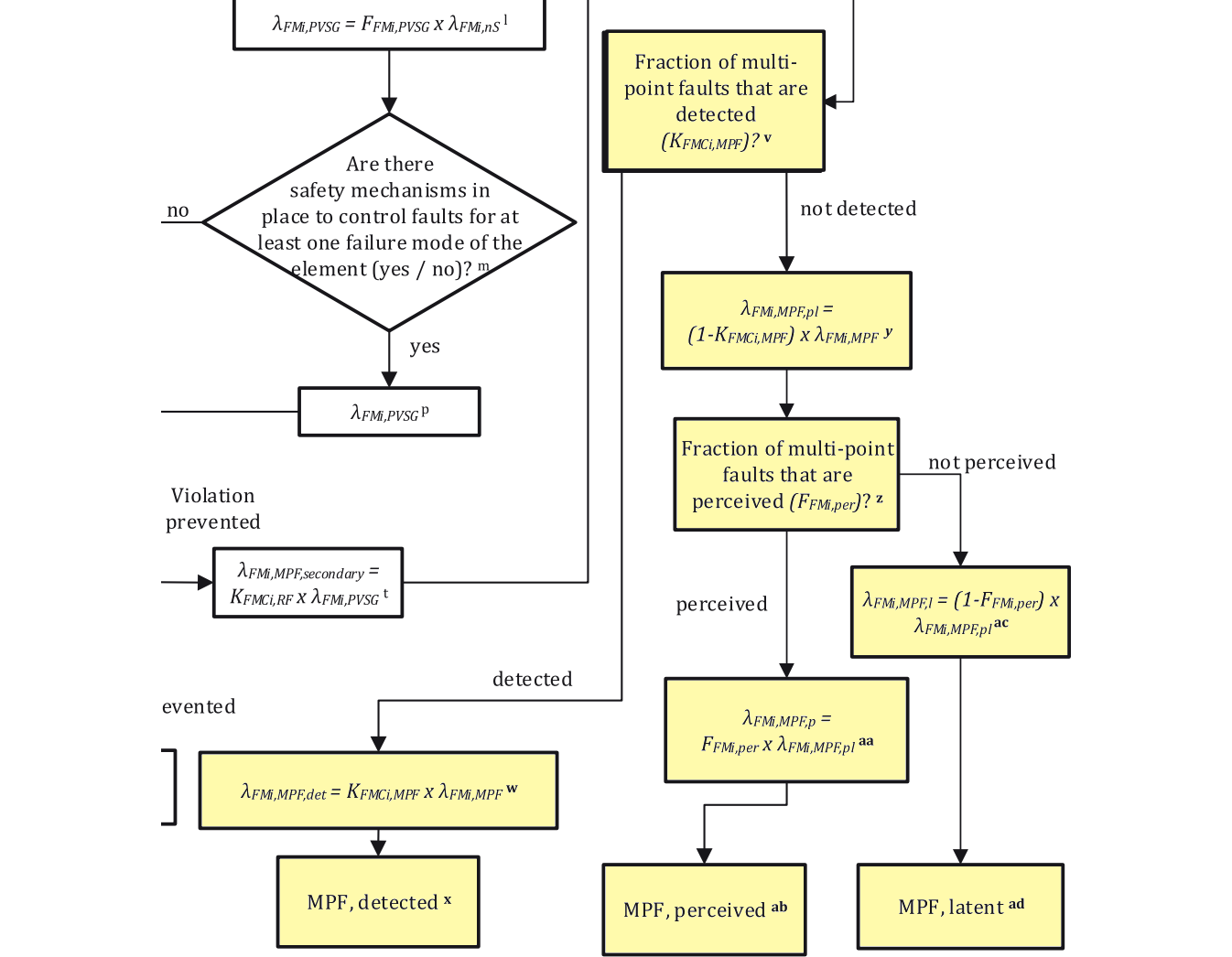 図174.1 Part 10故障分類フローチャート
図174.1 Part 10故障分類フローチャート
ドライバーに認識される場合は下に行き、箱(aa)により認識率$F_{FMC,per}$を掛けられ、その下の箱(ab)でMPF, perceived故障率として分類されます。
$$
\lambda_{FMi,MPF,p}=F_{FMC,per}\lambda_{FMi,MPF,pl}\tag{aa, ab}
$$
ドライバーに認識されない場合は右下に行き、箱(ac)において、不認識率$1-F_{FMC,per}$を掛けられ、その下の箱(ad)でMPF, latent故障率として分類されます。
$$
\lambda_{FMi,MPF,l}=(1-F_{FMC,per})\lambda_{FMi,MPF,pl}\tag{ac, ad}
$$
以上で全ての箱の説明が終了であり、以上による分類された故障率を用いて、SPFM、LFM、PMHFを計算することが可能です。
$\dagger$このMPF,detectedフォールトについてですが、1st Editionでは、MPF detectedフォールトがリペアされるのか、されないのか、レイテントなのか言及されていません。数学的な検証の結果、これはリペアされずLFになることが判明しています。一方、2nd Editionでは規格中にリペアされることが初めて言及されました(pattern 3)。これも数学的な検証の結果LFになることが判りました。このMPF detectedは、1st Edition、2nd Edition共LFになることが判明しているにも関わらず、LFMに含まれていないのは規格の矛盾と考えられます。
 前のブログ
次のブログ
前のブログ
次のブログ
posted by sakurai on October 25, 2019 #173
ニュースリリースでも明らかにしたように、このブログで研究してきたPMHFの一般式が、RAMS 2020に採択されました。ブログにおいて機能安全の知識は前提として良いので、注釈を取り除き、逆にブログとの関連の注釈☆をつけて再掲します。リリース文を茶色、注釈を青色で表示します。
なお、RAMS 2020に投稿中だったため、最新の研究#103~108を非開示としていましたが、今回採択が決定したので、RAMS 2020終了後(2020年2月頃)に公開予定です。

ISO 26262機能安全コンサルティングを提供するFSマイクロ株式会社(本社:名古屋市)代表取締役社長 桜井 厚の論文が、2019年10月19日、IEEE Reliability Society主催の国際学会である第66回RAMS(RAMS 2020)に採択されました。RAMS 2020は、2020年1月27日から30日まで、アメリカ・カリフォルニア州パームスプリングスのマリオット・ルネッサンスにて開催予定です。(☆1月30日最終日の12:15~14:15に開催されるコロキアムセッションにて発表します。)

論文の題名は「Generic Equations for a Probabilistic Metric for Random Hardware Failures According to ISO 26262」です。邦題は「ISO 26262に準拠したランダムハードウェア故障の確率的メトリクスの一般式」であり、ランダムハードウェア故障の確率的メトリクス(PMHF)を正確に評価することを可能にするものです。(☆上記にもあるように、本ブログでは#103~108で書きましたが、暫定非公開中です。⇒RAMS 2020が終了したので、当該記事を公開に変更しました。)
2011年に車載電子機器における機能安全の国際規格であるISO 26262の初版が、また、2018年には改訂版が発効されました。この規格改訂版においてはPMHF式が変更されていますが、PMHF値の数学的な定義や、エレメントの前提条件が明確ではありませんでした。(☆エレメントの前提条件とは具体的には修理可能性のことです。規格初版と規格改定版で、この修理可能性の前提を変えていると推測します。)
本論文ではこれらの点を明確にし、さらに規格に準拠した周期的な検査が行われるエレメントの不稼働確率式を初めて明らかにしました。
(☆不稼働確率については前記事に記載しています。)
これに基づき、一般的なサブシステムに関するPMHF式を新たに導出しました。本論文によりPMHF値を正確に評価できるため、広範な車載ECUにおいて、適正な安全設計を実施することが可能となります。また、緊急操作許容時間間隔(EOTTI)に関する過剰な設計制約を軽減できるため、自動運転システムに代表される耐故障システムにおいて、設計工期の短縮や製品コストの低減が可能となります。
(☆EOTTIの31倍の過剰見積もりについては前記事に記載しています。)
商号 FSマイクロ株式会社
代表者 桜井 厚
設立年月日 2013年8月21日
資本金 3,200万円
事業内容 ISO 26262車載電子機器の機能安全のコンサルティング及びセミナー
本店所在地 〒460-0011
愛知県名古屋市中区大須4-1-57
電話 052-263-3099
メールアドレス info@fs-micro.com
URL http://fs-micro.com
 前のブログ
次のブログ
前のブログ
次のブログ
posted by sakurai on October 25, 2019 #172
- 箱(q)ではVSGのprevention(防止、抑止)を聞いています。それも、菱形ではなく四角の判定箱なので、比率を聞いています。質問は、SMがVSGを抑止する割合$K_{FMCi,RF}$は?ということですが、$K_{FMCi,RF}$はフォールトした条件でのVSG抑止率である$\Pr\{\text{violation prevented}\ |\ \text{fault occured}\}$という条件付き確率となりそうですが、そうではないことを前記事で示しています。
VSG抑止できる部分(Violation prevented)は右に移動し、箱(t)で割合を掛けられ$\lambda_{FMi,MPF,secondary}$と名付けられます。
$$
\lambda_{FMi,MPF,secondary}=K_{FMCi,RF}\lambda_{FMi,PVSG}\tag{t}
$$
次に箱(u)で、$\lambda_{FMi,MPF,primary}$と加えられ、$\lambda_{FMi,MPF}$となります。
$$
\lambda_{FMi,MPF}=\lambda_{FMi,MPF,primary}+\lambda_{FMi,MPF,secondary}\tag{u}
$$
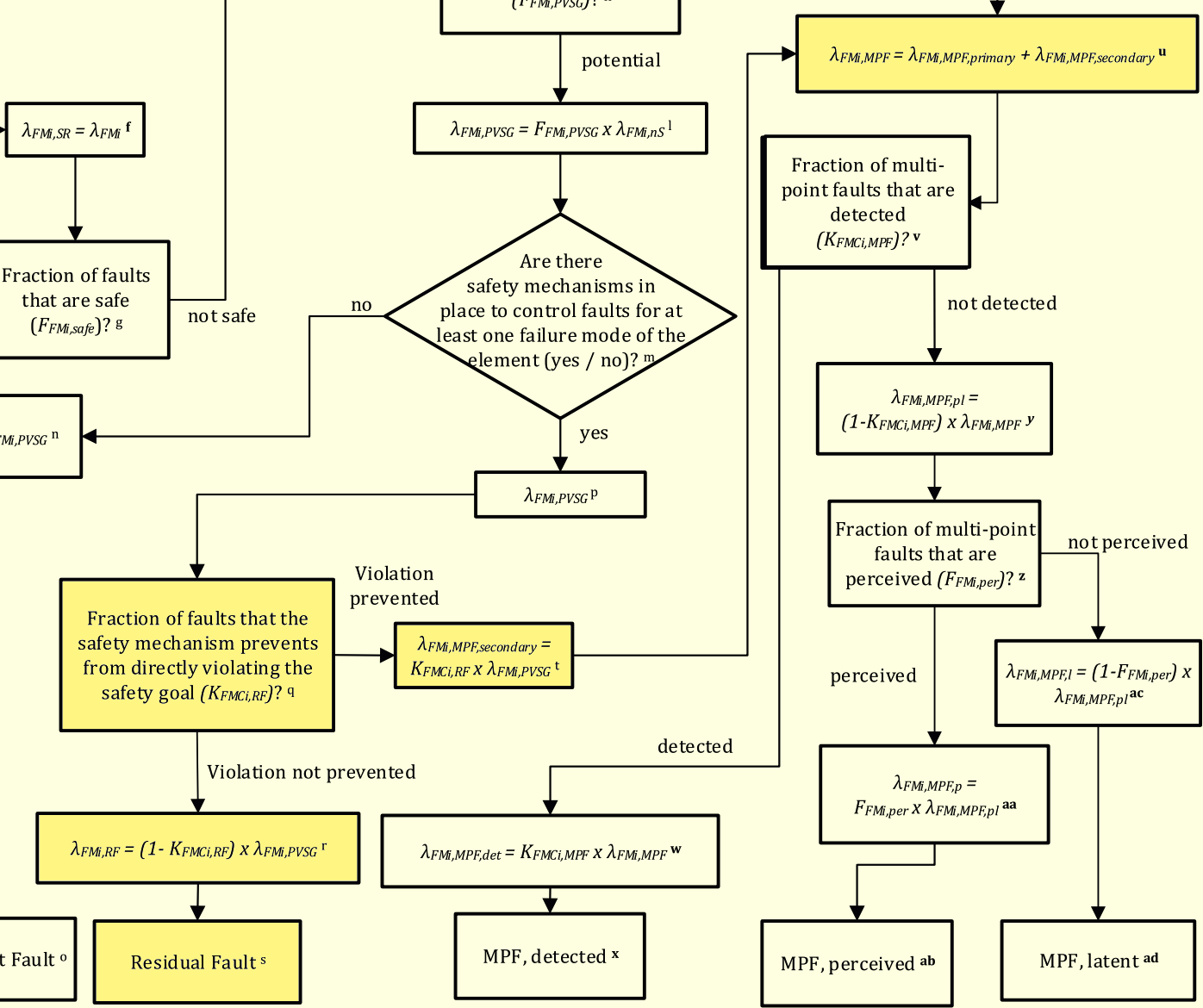 図172.1 Part 10故障分類フローチャート
図172.1 Part 10故障分類フローチャート
- 一方VSG抑止できない部分(Violation not prevented)は下に移動し、箱(r)で$1-K_{FMCi,RF}$を掛けられて下に移動し、箱(s)でResidual Fault故障率として分類されます。
$$
\lambda_{FMi,RF}=(1-K_{FMCi,RF})\lambda_{FMi,PVSG}\tag{r, s}
$$
 前のブログ
次のブログ
前のブログ
次のブログ
posted by sakurai on October 22, 2019 #171
- 箱(k)において、Part5のフローチャートでもあった、IFとSMの切り分けを行います。ただしいずれかの選択ではなく、割合を聞いています。SMを取り除いた場合に、どれだけの割合が直接VSGとなる可能性があるかという問いです。VSG可能性あり(potential)の場合は下に移動します。一方、VSG可能性無し(no potential)の場合は右に移動します。
下の箱(l)では、VSG可能性の割合$F_{FMi,PVSG}$を掛けて、VSG可能性の有る故障率$\lambda_{FMi,PVSG}$とします。
$$
\lambda_{FMi,PVSG}=F_{FMi,PVSG}\lambda_{FMi,nS}\tag{l}
$$
右の箱(ae)では、VSG可能性の無い割合$1-F_{FMi,PVSG}$を掛けて、VSG可能性の無い故障率$\lambda_{FMi,MPF,primary}$とします。$\dagger$
$$
\lambda_{FMi,MPF,primary}=(1-F_{FMi,PVSG})\lambda_{FMi,nS}\tag{ae}
$$
次の菱形(m)ではSMの有無を判定します。これは有無の選択なので、SMが無い場合(no)は左に移動します。
左の箱(n)ではSMが無い場合の故障率は$\lambda_{FMi,SPF}$と名付けられ、下に移動し、下の箱(o)でSingle Point Fault故障率として分類されます。
$$
\lambda_{FMi,SPF}=\lambda_{FMi,PVSG}\tag{n, o}
$$
一方、菱形(m)でSMが有る場合(Yes)には箱(p)に移動します。
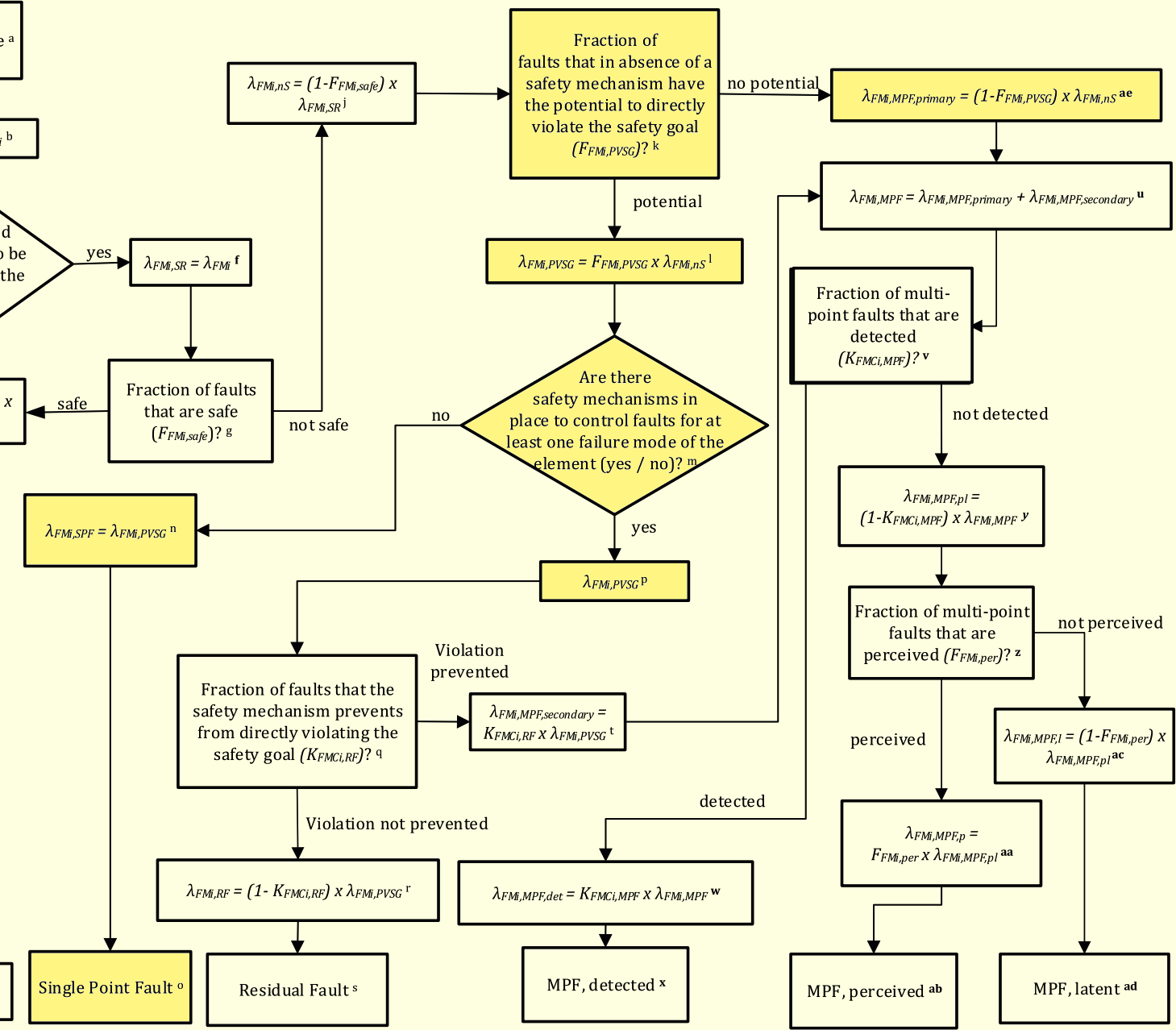 図171.1 Part 10故障分類フローチャート
図171.1 Part 10故障分類フローチャート
$\dagger$primary MPFもsecondary MPFも加え合わせるので、識別の必要は特にありませんが、SMのレイテントフォールト候補をprimary MPFと呼び、IFのレイテントフォールト候補をsecondary MPFと呼ぶようです。なぜここの箱の故障率がprimaryかと言えば、通常レイテントフォールト候補となる故障率はSMの故障だからだと推測します。
 前のブログ
次のブログ
前のブログ
次のブログ
posted by sakurai on October 17, 2019 #170
次の箱(g)はセーフフォルトの判定です。ここは菱形ではなく四角の箱であり、これは単純な選択ではなく、確率的に分類します。この場合だと、どれだけの割合が安全側かを聞いています。安全側(safe)と判断された故障率は左へ移動します。一方、非安全側(not safe)と判定された故障率は、右上の箱(i)に移動します。
左の箱(h)において、安全側の割合($F_{FM,safe}$)を掛け、$\lambda_{FM,S}$と名付けられます。それがそのまま下に移動して、箱(i)でSafe fault故障率として分類されます。この故障率は分析に使用されます。
$$
\lambda_{FMi,S}=F_{FM,safe}\lambda_{FMi,SR}\tag{h, i}
$$
右上の箱(j)において、非安全側の割合($1-F_{FM,safe}$)を掛け、$\lambda_{FM,nS}$と名付けられます。
$$
\lambda_{FMi,nS}=(1-F_{FM,safe})\lambda_{FMi,SR}\tag{j}
$$
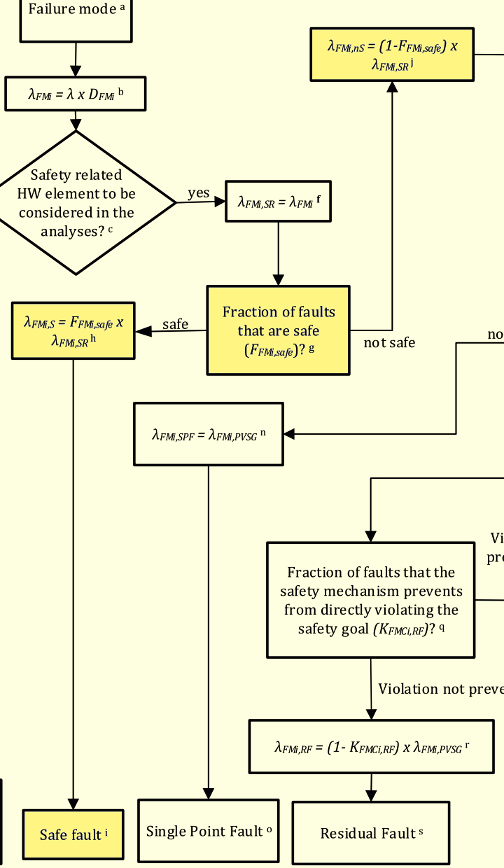 図170.1 Part 10故障分類フローチャート
図170.1 Part 10故障分類フローチャート
 前のブログ
次のブログ
前のブログ
次のブログ
posted by sakurai on October 16, 2019 #169
Part 10の故障分類フローチャートもPart 5の故障分類フローチャートと同様、故障率データベースや信頼性試験で得られた要素故障率に基づき、故障率を分類していきます。Part 5のフローチャートでは故障率を入力しているものの、数式が無いため定量計算ができませんでしたが、Part 10のフローチャートでは、定量計算を実施します。
- 左上のボックス(a)から、要素故障率$\lambda$を入力します。全ての部品の全ての故障モードに関する故障率を入力します。
- 箱(b)において、故障率分配($D_{FMi}$)が掛けられ、故障モードの故障率$\lambda_{FMi}$となります。
$$
\lambda_{FMi}=D_{FMi}\lambda\tag{b}
$$
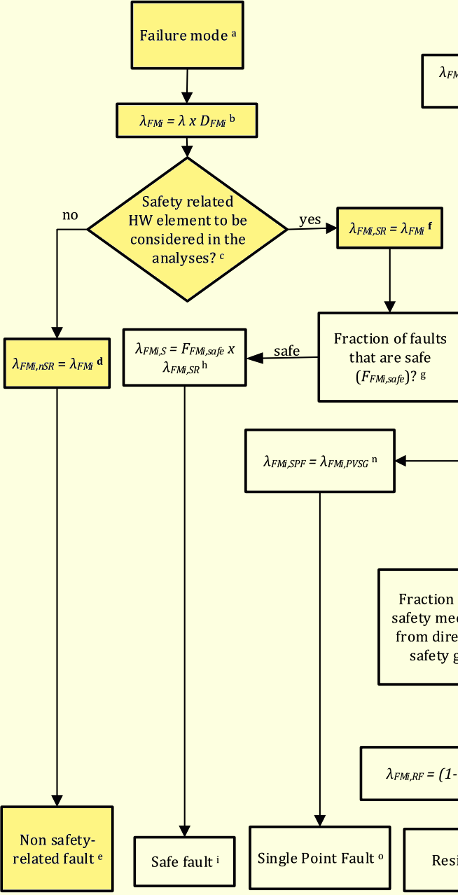 図169.1 Part 10故障分類フローチャート
図169.1 Part 10故障分類フローチャート
菱形(c)の判定では、エレメントないし故障モードが安全関連かどうかを判定します。以前にも述べたように、例えばデバッグ回路のように運転中に動作しない場合に限り、非安全関連(No)と分類できます。他の回路は通常、安全関連(Yes)と分類されます。
非安全関連(No)の場合は左下に移動し、箱(d)で$\lambda_{FMi,nSR}$となり、箱(e)で非安全関連フォールトnSR故障率と分類されます。この故障率は分析には使用されません。
$$
\lambda_{FMi,nSR}=\lambda_{FMi}\tag{d, e}
$$
一方、菱形(c)で安全関連(Yes)と判定された故障率は、右に移動し、箱(f)で新たに$\lambda_{FMi,SR}$と名付けられます。
$$
\lambda_{FMi,SR}=\lambda_{FMi}\tag{f}
$$
 前のブログ
次のブログ
前のブログ
次のブログ
posted by sakurai on October 15, 2019 #168
Part 5のフローチャートの次にPart 10 Figure 1を解説します。基本的な流れはPart 5のFigure B.2と同じです。
以下の図にPart 10の故障分類フローチャートの全体図を示します。Part 5の図と違う点は、
- 個々のボックスに符号(アルファベット)が振ってあり、それによりどのボックスか明確に指示できる
- 全てのボックスに数式やパラメータが明示されており、どの値をどのように計算するのかが定量的に書かれている
の2点です。
従って、Part 5の故障分類フローチャートは定性的に理解し、Part 10の故障分類フローチャートは定量的に理解することになります。FSマイクロでは、このPart 10の故障分類フローチャートをメインに考えて行きます。
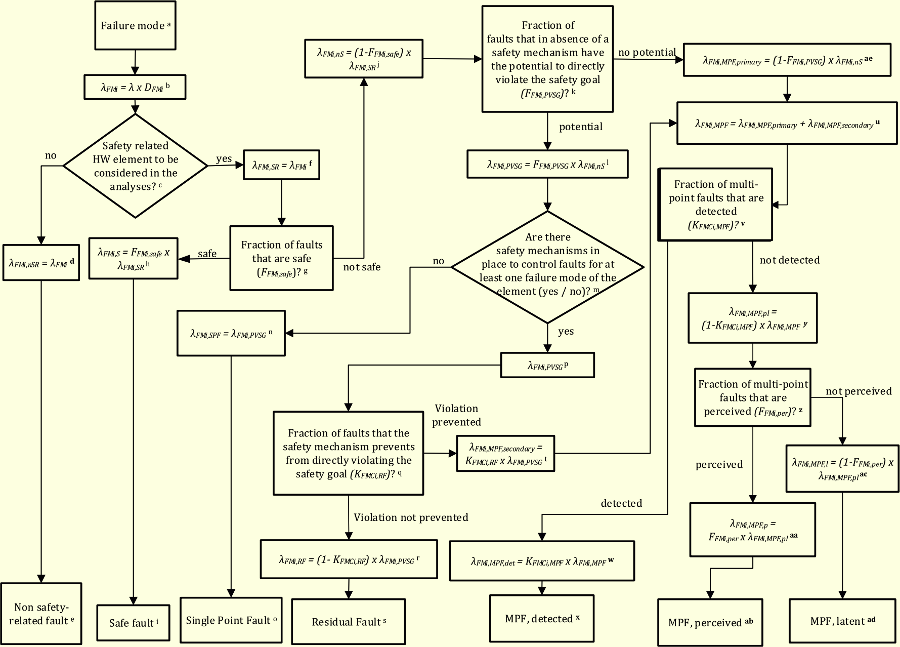 図168.1 Part 10故障分類フローチャート
図168.1 Part 10故障分類フローチャート
 前のブログ
次のブログ
前のブログ
次のブログ
posted by sakurai on October 14, 2019 #167
前稿で、IFとSMの判定の菱形と説明した判定において、VSGの可能性無し(no)の場合は右側に移動します。さらに、VSGの可能性が有るがSMでカバーされる部分の故障も、下方からここへ合流します。
次の菱形はDPFの可能性が有るかどうかの判定です。ここに来る場合は単独でのVSGの可能性無しのSMの場合ですが、組み合わせてVSGにならない場合はISO 26262の範囲外(No)として右下に移動し、S (Safe Fault)と分類されます。一方、他のフォールト、通常はIFのフォールトとの組み合わせでVSGとなる場合(Yes)は下に移動します。
次の菱形は、レイテントフォールト防止のSMがあるか、あるいはドライバーにより認識されるかどうかの判定であり、どちらかがYesであれば、レイテントフォールトとはなりません。両方共Noの場合、つまりレイテントフォールト防止SMが無く、かつドライバーに認識されなければ左下に移動し、レイテントフォールトMPF,L(LはLatentの意味)と判定されます。一方、どちらかがYesの場合は下に移動します。
次の円形の判断においては、レイテントフォールト防止カバレージの値が問題になります。ここは定量的な質問であり、レイテントフォールトが防止される割合分の故障は下に移動し、MPF,DP(DPとはdetected or percievedの意味)と判定されます。逆に、レイテントフォールトが防止されない割合分の故障は左下に移動し、MPF,L(atent)と判定されます。
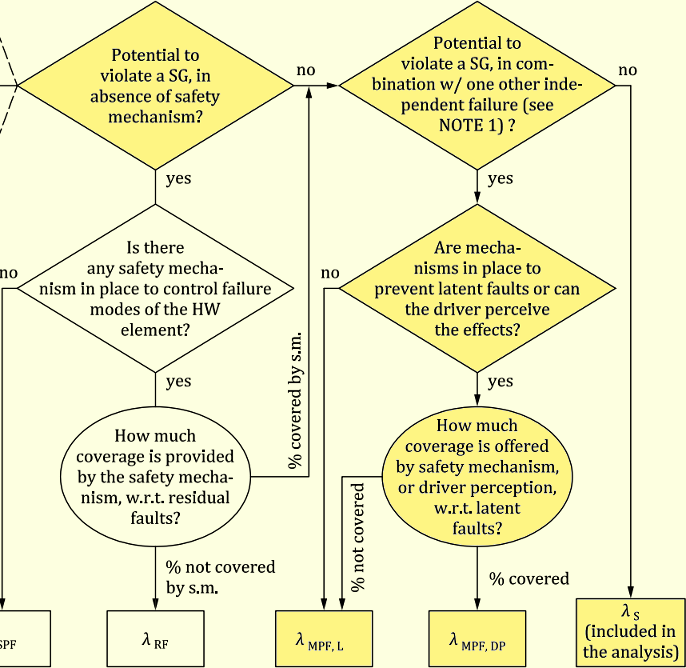 図167.1 Part 5故障分類フローチャート
図167.1 Part 5故障分類フローチャート
 前のブログ
次のブログ
前のブログ
次のブログ
ページ:












